Single Polymer problems
 Our group has, in recent years, implemented a rigorous statistical mechanics scheme to treat phenomena occuring in single polymer molecules. One starts with ab-initio calculations of small units of the polymer in question, which generally encompass only a few monomer units. These studies are used to obtain geometric and energetic data on a conformer or conformer combination basis. Using the Transfer Matrix, or TM approach (see below), we are able to calculate virtually any property of a given molecular model. We have used our theory primarily to model molecules like alkanes, via the Rotationally Isomeric State model and generalizations thereof, as well as polyethylene glycol (PEG). The latter requires a detailed polymer model where we take into account interactions up to nine bonds along the backbone. This theory has led to a parameter-free fit of the observed force-extension curves in long PEG molecules.
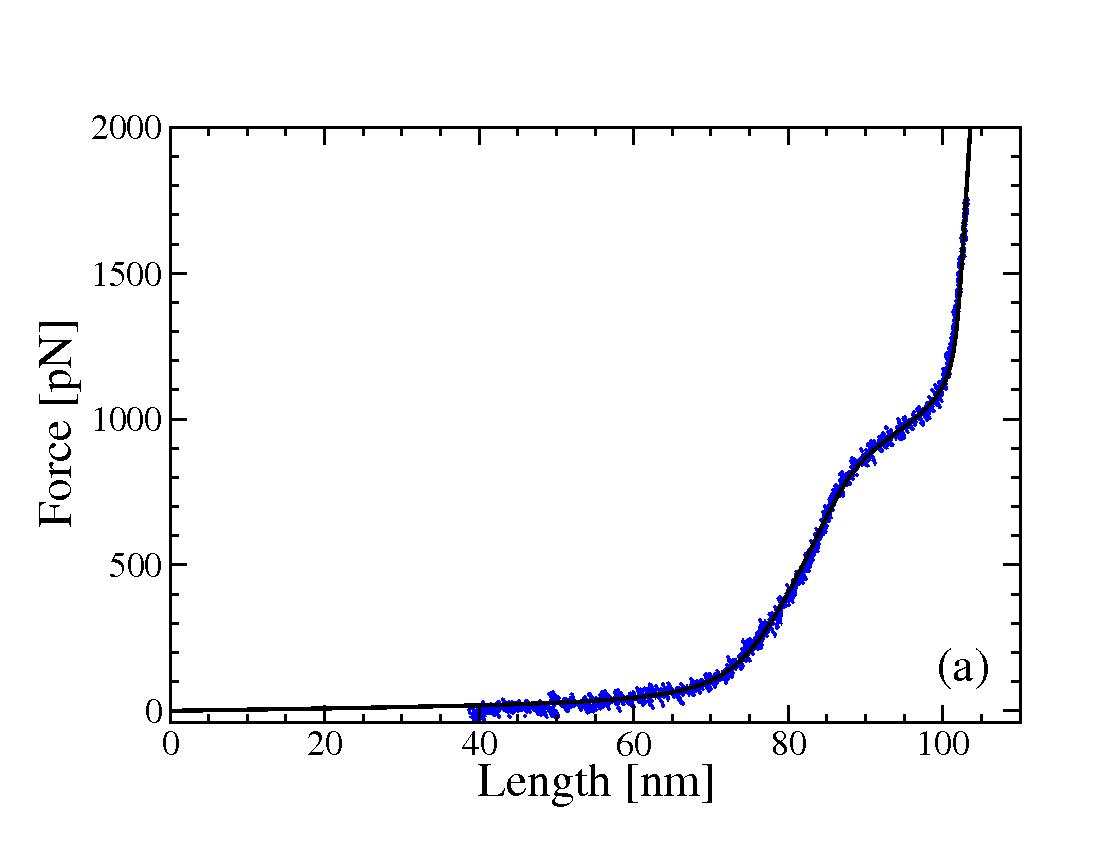
Shown in the figure (right) is the force extension curve (both theory and experiment) of a Dextran strand with 175 monomers. The theory (black) is based on the continuous two-state model, presented in:
F. Hanke and H.J. Kreuzer. Conformational transitions in
single polymer molecules modeled with a complete energy landscape:
continuous two-state model. Eur. Phys. J. E 22, 163-169 (2007).
Our group has, in recent years, implemented a rigorous statistical mechanics scheme to treat phenomena occuring in single polymer molecules. One starts with ab-initio calculations of small units of the polymer in question, which generally encompass only a few monomer units. These studies are used to obtain geometric and energetic data on a conformer or conformer combination basis. Using the Transfer Matrix, or TM approach (see below), we are able to calculate virtually any property of a given molecular model. We have used our theory primarily to model molecules like alkanes, via the Rotationally Isomeric State model and generalizations thereof, as well as polyethylene glycol (PEG). The latter requires a detailed polymer model where we take into account interactions up to nine bonds along the backbone. This theory has led to a parameter-free fit of the observed force-extension curves in long PEG molecules.
Shown in the figure (right) is the force extension curve (both theory and experiment) of a Dextran strand with 175 monomers. The theory (black) is based on the continuous two-state model, presented in:
F. Hanke and H.J. Kreuzer. Conformational transitions in
single polymer molecules modeled with a complete energy landscape:
continuous two-state model. Eur. Phys. J. E 22, 163-169 (2007).
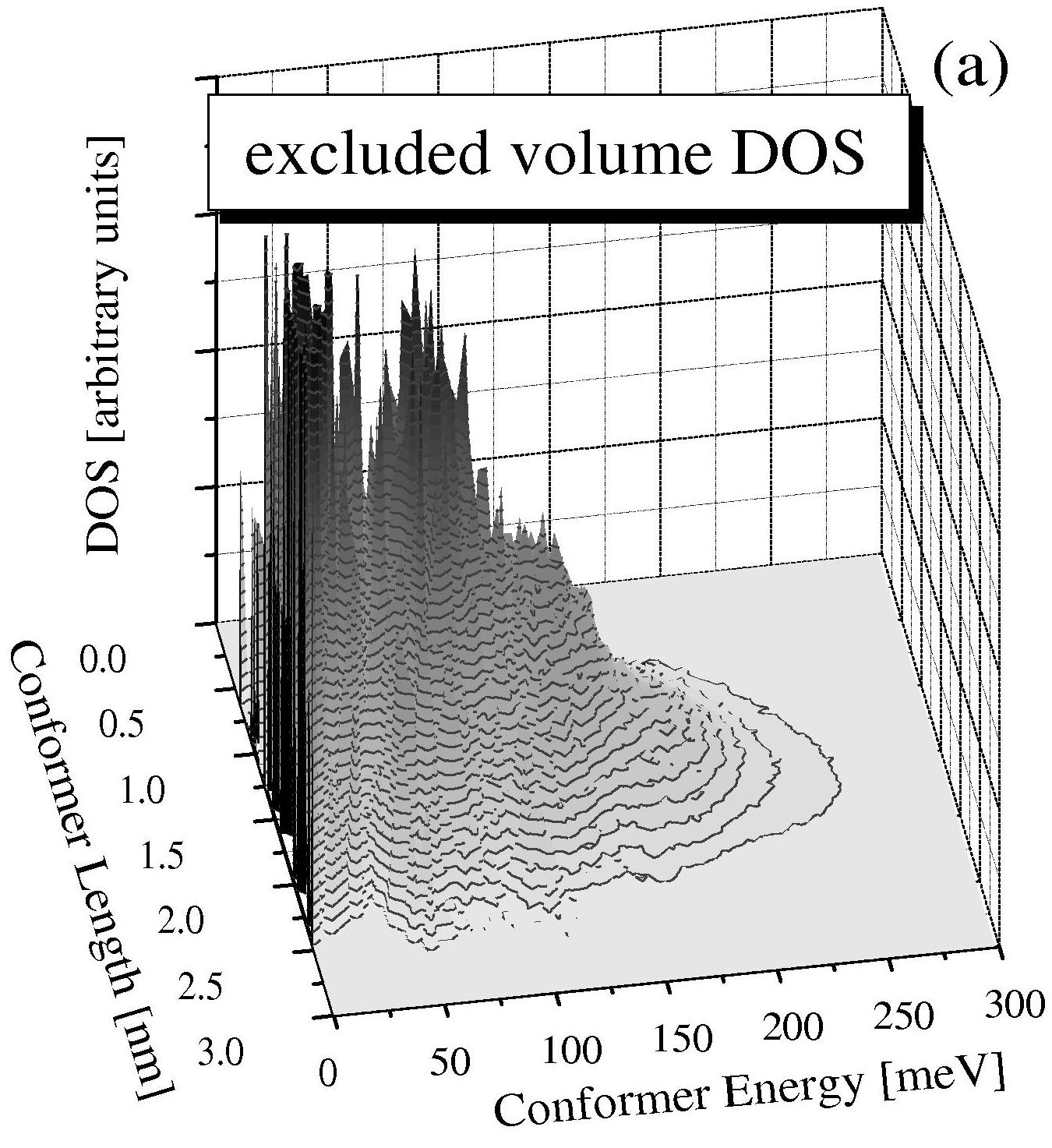
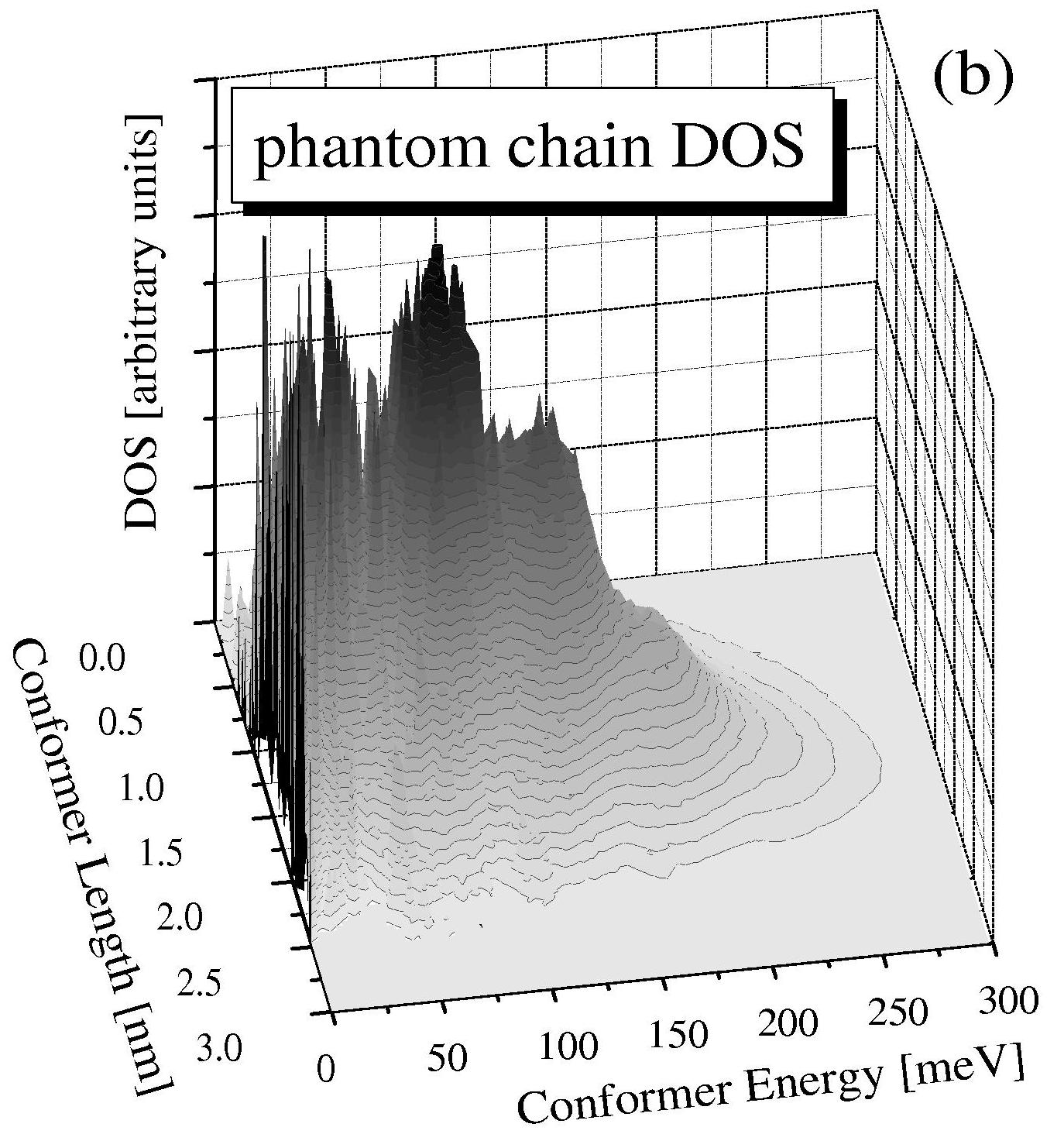
Shown above is the complete Density of states for a poly (ethylene glycol) molecule of seven repeat units with a total of more than ten billion conformers.
Calculations are compared with and without Excluded Volume (EV) interactions; the complete discussion of this calculation is available in:
Douglas Staple, Felix Hanke, and H.J. Kreuzer. Complete free
energy landscape and statistical thermodynamics of single poly(ethylene
glycol) molecules. New J. Physics 9, 68 1-18 (2007).
Other areas of polymer research is the interaction of self-assembled monolayers with water and the modification of polymers in high electric fields. More recently we have looked at more complicated systems such as the boat-chair transition in the polysaccharide Dextran, the stretching of Titin and the response of intermediate filaments in muscles. Again, the Transfer Matrix method is used to great advantage. To address the overriding question whether stretching with an Atomic Force Microscope takes a polymer molecule out of equilibrium we have developed a non-equilibrium theory of polymer stretching based on the master equation. The stretching of DNA is next.

